diff --git a/code/elements.json b/code/elements.json
new file mode 100644
index 0000000000000000000000000000000000000000..2560686444bbe5b99443613a9c414ecccf11f191
--- /dev/null
+++ b/code/elements.json
@@ -0,0 +1 @@
+[{"number": 1, "abbr": "H", "full_name": "hydrogen", "remark": "(H 2 , gas)", "c": 28.836}, {"number": 2, "abbr": "He", "full_name": "helium", "remark": "(gas)", "c": 20.786}, {"number": 3, "abbr": "Li", "full_name": "lithium", "remark": "", "c": 24.86}, {"number": 4, "abbr": "Be", "full_name": "beryllium", "remark": "", "c": 16.443}, {"number": 5, "abbr": "B", "full_name": "boron", "remark": "(rhombic)", "c": 11.087}, {"number": 6, "abbr": "C", "full_name": "carbon", "remark": "(graphite)", "c": 8.517}, {"number": 6, "abbr": "C", "full_name": "carbon", "remark": "(diamond, nonstd state)", "c": 6.115}, {"number": 7, "abbr": "N", "full_name": "nitrogen", "remark": "(N 2 , gas)", "c": 29.124}, {"number": 8, "abbr": "O", "full_name": "oxygen", "remark": "(O 2 , gas)", "c": 29.378}, {"number": 9, "abbr": "F", "full_name": "fluorine", "remark": "(F 2 , gas)", "c": 31.304}, {"number": 10, "abbr": "Ne", "full_name": "neon", "remark": "(gas)", "c": 20.786}, {"number": 11, "abbr": "Na", "full_name": "sodium", "remark": "", "c": 28.23}, {"number": 12, "abbr": "Mg", "full_name": "magnesium", "remark": "", "c": 24.869}, {"number": 13, "abbr": "Al", "full_name": "aluminium", "remark": "", "c": 24.2}, {"number": 14, "abbr": "Si", "full_name": "silicon", "remark": "", "c": 19.789}, {"number": 15, "abbr": "P", "full_name": "phosphorus", "remark": "(white)", "c": 23.824}, {"number": 15, "abbr": "P", "full_name": "phosphorus", "remark": "(red, nonstd state)", "c": 21.19}, {"number": 16, "abbr": "S", "full_name": "sulfur", "remark": "(rhombic)", "c": 22.75}, {"number": 16, "abbr": "S", "full_name": "sulfur", "remark": "(monoclinic, nonstd state)", "c": 23.23}, {"number": 17, "abbr": "Cl", "full_name": "chlorine", "remark": "(Cl 2 gas)", "c": 33.949}, {"number": 18, "abbr": "Ar", "full_name": "argon", "remark": "(gas)", "c": 20.786}, {"number": 19, "abbr": "K", "full_name": "potassium", "remark": "", "c": 29.6}, {"number": 20, "abbr": "Ca", "full_name": "calcium", "remark": "", "c": 25.929}, {"number": 21, "abbr": "Sc", "full_name": "scandium", "remark": "", "c": 25.52}, {"number": 22, "abbr": "Ti", "full_name": "titanium", "remark": "", "c": 25.06}, {"number": 23, "abbr": "V", "full_name": "vanadium", "remark": "", "c": 24.89}, {"number": 24, "abbr": "Cr", "full_name": "chromium", "remark": "", "c": 23.35}, {"number": 25, "abbr": "Mn", "full_name": "manganese", "remark": "", "c": 26.32}, {"number": 26, "abbr": "Fe", "full_name": "iron", "remark": "(alpha)", "c": 25.1}, {"number": 27, "abbr": "Co", "full_name": "cobalt", "remark": "", "c": 24.81}, {"number": 28, "abbr": "Ni", "full_name": "nickel", "remark": "", "c": 26.07}, {"number": 29, "abbr": "Cu", "full_name": "copper", "remark": "", "c": 24.44}, {"number": 30, "abbr": "Zn", "full_name": "zinc", "remark": "", "c": 25.39}, {"number": 31, "abbr": "Ga", "full_name": "gallium", "remark": "", "c": 25.86}, {"number": 32, "abbr": "Ge", "full_name": "germanium", "remark": "", "c": 23.222}, {"number": 33, "abbr": "As", "full_name": "arsenic", "remark": "(alpha, gray)", "c": 24.64}, {"number": 34, "abbr": "Se", "full_name": "selenium", "remark": "(hexagonal)", "c": 25.363}, {"number": 35, "abbr": "Br", "full_name": "bromine", "remark": "", "c": 75.69}, {"number": 36, "abbr": "Kr", "full_name": "krypton", "remark": "(gas)", "c": 20.786}, {"number": 37, "abbr": "Rb", "full_name": "rubidium", "remark": "", "c": 31.06}, {"number": 38, "abbr": "Sr", "full_name": "strontium", "remark": "", "c": 26.4}, {"number": 39, "abbr": "Y", "full_name": "yttrium", "remark": "", "c": 26.53}, {"number": 40, "abbr": "Zr", "full_name": "zirconium", "remark": "", "c": 25.36}, {"number": 41, "abbr": "Nb", "full_name": "niobium", "remark": "", "c": 24.6}, {"number": 42, "abbr": "Mo", "full_name": "molybdenum", "remark": "", "c": 24.06}, {"number": 43, "abbr": "Tc", "full_name": "technetium", "remark": "", "c": 24.27}, {"number": 44, "abbr": "Ru", "full_name": "ruthenium", "remark": "", "c": 24.06}, {"number": 45, "abbr": "Rh", "full_name": "rhodium", "remark": "", "c": 24.98}, {"number": 46, "abbr": "Pd", "full_name": "palladium", "remark": "", "c": 25.98}, {"number": 47, "abbr": "Ag", "full_name": "silver", "remark": "", "c": 25.35}, {"number": 48, "abbr": "Cd", "full_name": "cadmium", "remark": "", "c": 26.02}, {"number": 49, "abbr": "In", "full_name": "indium", "remark": "", "c": 26.74}, {"number": 50, "abbr": "Sn", "full_name": "tin", "remark": "(white)", "c": 27.112}, {"number": 50, "abbr": "Sn", "full_name": "tin", "remark": "(gray, nonstd state)", "c": 25.77}, {"number": 51, "abbr": "Sb", "full_name": "antimony", "remark": "", "c": 25.23}, {"number": 52, "abbr": "Te", "full_name": "tellurium", "remark": "", "c": 25.73}, {"number": 53, "abbr": "I", "full_name": "iodine", "remark": "", "c": 54.44}, {"number": 54, "abbr": "Xe", "full_name": "xenon", "remark": "(gas)", "c": 20.786}, {"number": 55, "abbr": "Cs", "full_name": "caesium", "remark": "", "c": 32.21}, {"number": 56, "abbr": "Ba", "full_name": "barium", "remark": "", "c": 28.07}, {"number": 57, "abbr": "La", "full_name": "lanthanum", "remark": "", "c": 27.11}, {"number": 58, "abbr": "Ce", "full_name": "cerium", "remark": "(gamma, fcc)", "c": 26.94}, {"number": 59, "abbr": "Pr", "full_name": "praseodymium", "remark": "", "c": 27.2}, {"number": 60, "abbr": "Nd", "full_name": "neodymium", "remark": "", "c": 27.45}, {"number": 62, "abbr": "Sm", "full_name": "samarium", "remark": "", "c": 29.54}, {"number": 63, "abbr": "Eu", "full_name": "europium", "remark": "", "c": 27.66}, {"number": 64, "abbr": "Gd", "full_name": "gadolinium", "remark": "", "c": 37.03}, {"number": 65, "abbr": "Tb", "full_name": "terbium", "remark": "", "c": 28.91}, {"number": 66, "abbr": "Dy", "full_name": "dysprosium", "remark": "", "c": 27.7}, {"number": 67, "abbr": "Ho", "full_name": "holmium", "remark": "", "c": 27.15}, {"number": 68, "abbr": "Er", "full_name": "erbium", "remark": "", "c": 28.12}, {"number": 69, "abbr": "Tm", "full_name": "thulium", "remark": "", "c": 27.03}, {"number": 70, "abbr": "Yb", "full_name": "ytterbium", "remark": "", "c": 26.74}, {"number": 71, "abbr": "Lu", "full_name": "lutetium", "remark": "", "c": 26.86}, {"number": 72, "abbr": "Hf", "full_name": "hafnium", "remark": "(hexagonal)", "c": 25.73}, {"number": 73, "abbr": "Ta", "full_name": "tantalum", "remark": "", "c": 25.36}, {"number": 74, "abbr": "W", "full_name": "tungsten", "remark": "", "c": 24.27}, {"number": 75, "abbr": "Re", "full_name": "rhenium", "remark": "", "c": 25.48}, {"number": 76, "abbr": "Os", "full_name": "osmium", "remark": "", "c": 24.7}, {"number": 77, "abbr": "Ir", "full_name": "iridium", "remark": "", "c": 25.1}, {"number": 78, "abbr": "Pt", "full_name": "platinum", "remark": "", "c": 25.86}, {"number": 79, "abbr": "Au", "full_name": "gold", "remark": "", "c": 25.418}, {"number": 80, "abbr": "Hg", "full_name": "mercury", "remark": "(liquid)", "c": 27.983}, {"number": 81, "abbr": "Tl", "full_name": "thallium", "remark": "", "c": 26.32}, {"number": 82, "abbr": "Pb", "full_name": "lead", "remark": "", "c": 26.65}, {"number": 83, "abbr": "Bi", "full_name": "bismuth", "remark": "", "c": 25.52}, {"number": 84, "abbr": "Po", "full_name": "polonium", "remark": "", "c": 26.4}, {"number": 86, "abbr": "Rn", "full_name": "radon", "remark": "(gas)", "c": 20.786}, {"number": 87, "abbr": "Fr", "full_name": "francium", "remark": "", "c": 31.8}, {"number": 89, "abbr": "Ac", "full_name": "actinium", "remark": "", "c": 27.2}, {"number": 90, "abbr": "Th", "full_name": "thorium", "remark": "", "c": 26.23}, {"number": 92, "abbr": "U", "full_name": "uranium", "remark": "", "c": 27.665}, {"number": 93, "abbr": "Np", "full_name": "neptunium", "remark": "", "c": 29.46}, {"number": 94, "abbr": "Pu", "full_name": "plutonium", "remark": "", "c": 35.5}, {"number": 95, "abbr": "Am", "full_name": "americium", "remark": "", "c": 62.7}]
\ No newline at end of file
diff --git a/code/scrape_wiki.py b/code/scrape_wiki.py
new file mode 100644
index 0000000000000000000000000000000000000000..a561871943eb303a3b1fa81fc616e4a403f97294
--- /dev/null
+++ b/code/scrape_wiki.py
@@ -0,0 +1,44 @@
+# -*- coding: utf-8 -*-
+# ---
+# jupyter:
+# jupytext:
+# text_representation:
+# extension: .py
+# format_name: light
+# format_version: '1.3'
+# jupytext_version: 0.8.6
+# kernelspec:
+# display_name: Python 3
+# language: python
+# name: python3
+# ---
+
+# +
+from pathlib import Path
+import json
+
+import wikitables
+
+raw, = wikitables.import_tables('Heat capacities of the elements (data page)')
+
+# +
+elements = []
+for index, row in enumerate(raw.rows):
+ if not row[''].value.startswith('<'):
+ continue
+ description = row[''].value
+ description = description[description.index('>') + 2:]
+ c = raw.rows[index+1]['J/(mol·K)'].value
+ if not isinstance(c, float):
+ c = float(c.split()[-1])
+ number, abbr, full_name, *remark = description.split()
+ element = {
+ 'number': int(number),
+ 'abbr': abbr,
+ 'full_name': full_name,
+ 'remark': ' '.join(remark),
+ 'c': c,
+ }
+ elements.append(element)
+
+Path('elements.json').write_text(json.dumps(elements))
diff --git a/src/1_einstein_model.md b/src/1_einstein_model.md
index a36e2a2a0159d7a7da93d47865e8f95eb42ec368..b2b75cc6ee4c5f6c9fac715241d3c5ba1d753e14 100644
--- a/src/1_einstein_model.md
+++ b/src/1_einstein_model.md
@@ -13,11 +13,15 @@ jupyter:
---
```python
-from matplotlib import pyplot
+import pandas
+from matplotlib import pyplot
import numpy as np
from scipy.optimize import curve_fit
from scipy.integrate import quad
+import plotly.offline as py
+import plotly.graph_objs as go
+
from common import draw_classic_axes, configure_plotting
@@ -34,26 +38,59 @@ _(based on chapter 2.1 of the book)_
- Compute the expected particle number, energy, and heat capacity of a quantum harmonic oscillator (a single boson)
- Write down the total thermal energy of a material
-## Einstein model
-### Classical limit
+## Classical limit of heat capacity
-An empirical observation:
+Let us look at the heat capacities of different chemical elements[^1]:
-> The law of Dulong-Petit (1819): In most materials heat capacity per atom $C \approx 3k_B$
+```python
+elements = pandas.read_json('elements.json')
+elements.full_name = elements.full_name.str.capitalize()
+hovertext = elements.T.apply(
+ lambda s: f'<sup>{s.number}</sup>{s.abbr} '
+ f'[{s.full_name}{", " * bool(s.remark)}{s.remark}]'
+)
+
+fig = go.Figure(
+ data=[
+ go.Scatter(
+ x=elements.number,
+ y=elements.c / 8.314,
+ mode='markers+text',
+ textposition='top center',
+ hovertext=hovertext,
+ hoverinfo='text'
+ ),
+ ],
+ layout=go.Layout(
+ title='Heat capacity of chemical elements',
+ autosize=True,
+ yaxis=go.layout.YAxis(
+ title='$C/k_B$',
+ tick0=1,
+ dtick=2,
+ ),
+ xaxis=go.layout.XAxis(
+ title='Atomic number'
+ ),
+ hovermode='closest',
+ ),
+)
+
+py.iplot(fig, show_link=False)
+```
-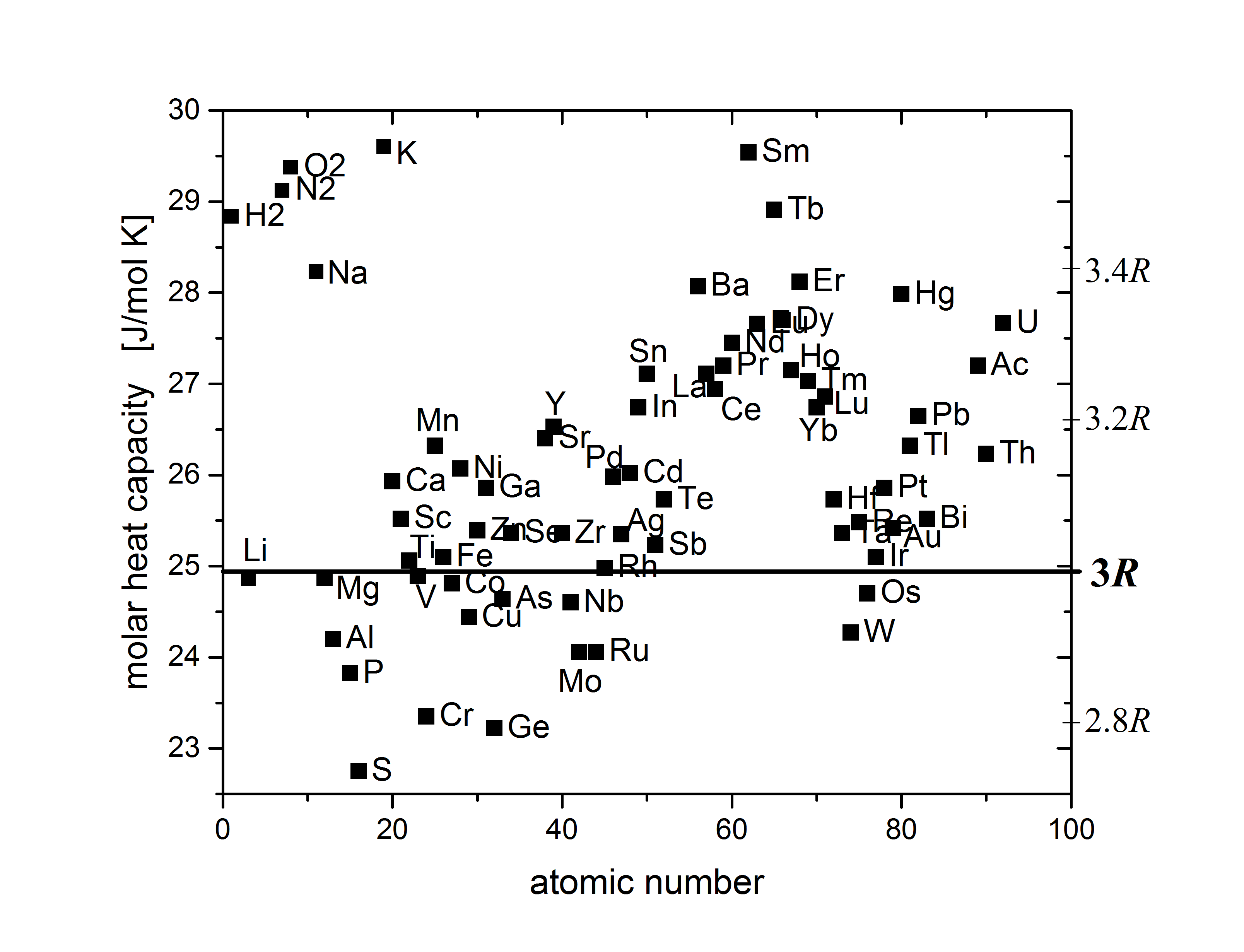
+An empirical observation, also known as the **law of Dulong–Petit** (1819):
-??? info "source"
+> In most materials heat capacity per atom $C \approx 3k_B$
- By Nick B. - Own work, [CC BY-SA 4.0](https://creativecommons.org/licenses/by-sa/4.0 "Creative Commons Attribution-Share Alike 4.0"), [Link](https://commons.wikimedia.org/w/index.php?curid=54031939)
+This corresponds to what we know from statictical physics and the equipartition theorem: every atom has 3 momenta and 3 coordinates.
+The equipartition theorem states that each of these 6 degrees of freedom contributes $k_B/2$ to the heat capacity.
-To explain assume that each atom is a classical harmonic oscillator in 3D.
-This gives 6 degrees of freedom, each contributing $k_B/2$ to the heat capacity.
-### Problem
+### Complication
-Experiments showed that this law breaks down at low temperatures, so Einstein was facing the mystery of this measurement:
+Things start looking more complex when we study (following Einstein) the temperature dependence of the heat capacity of diamond[^2]:
```python
# Data from Einstein's paper
@@ -67,13 +104,14 @@ ax.set_ylabel('$C/k_B$')
ax.set_ylim((0, 3));
```
-So there is:
+So we see that:
-* Strong temperature dependence of $C$
* At high temperature the law of Dulong–Petit works
+* Strong temperature dependence of $C$
* At low $T$, $C \rightarrow 0$
-### Quantum oscillator
+
+## Quantum oscillator
This can be explained by considering a _quantum_ harmonic oscillator:
@@ -82,30 +120,30 @@ import math
from numpy.polynomial.hermite import Hermite
def ho_evec(x, n, no_states):
-
+
"""
Calculate the wavefunction of states confined in the harmonic oscillator
-
+
Input:
------
x: numpy array of x coordinates (in units of hbar.omega)
n: n^th bound state in the oscillator
no_states: no of states confined
-
+
Returns:
--------
Wavefunctions
-
+
"""
-
+
# calculate hermite polynomial
vec = [0] * no_states
vec[n] = 1/2
Hn = Hermite(vec)
-
- return ((1/np.sqrt(math.factorial(n)*2**n))*
- pow(np.pi,-1/4)*
- np.exp(-pow(x, 2)/2)*
+
+ return ((1/np.sqrt(math.factorial(n)*2**n))*
+ pow(np.pi,-1/4)*
+ np.exp(-pow(x, 2)/2)*
Hn(x))
def h0_ener(n):
@@ -113,7 +151,7 @@ def h0_ener(n):
Calculate the energy of nth bound state
"""
return (n + 1/2)
-
+
x = np.linspace(-4, 4, 100) #units of hbar.omega
no_states = 7 #no of bound states confined in the quantum well
@@ -123,36 +161,36 @@ V = 0.5*(omega**2)*(x**2)
fig, ax = pyplot.subplots(figsize=(10, 7))
for i in range(no_states):
-
+
ax.hlines(h0_ener(i), x[0], x[len(x)-1], linestyles='dotted', colors='k')
-
+
ax.plot(x, ho_evec(x, i, no_states) + h0_ener(i)) #plot wavefunctions
-
-
+
+
# annotate plot
- ax.text(x[len(x)-1], h0_ener(i)+1/4, r'$\Psi_%2i (x)$' %(i),
+ ax.text(x[len(x)-1], h0_ener(i)+1/4, r'$\Psi_%2i (x)$' %(i),
horizontalalignment='center', fontsize=14)
-
- ax.text(1/4, h0_ener(i)+1/4, '$E_%2i$' %(i),
+
+ ax.text(1/4, h0_ener(i)+1/4, '$E_%2i$' %(i),
horizontalalignment='center', fontsize=14)
-
- if i==0:
- ax.text(x[0]+1/4, h0_ener(i)/4, r'$\frac{\hbar\omega}{2}$',
+
+ if i==0:
+ ax.text(x[0]+1/4, h0_ener(i)/4, r'$\frac{\hbar\omega}{2}$',
horizontalalignment='center', fontsize=14)
-
- ax.annotate("", xy=(x[0]+1/2, h0_ener(i)-1/2),
- xytext=(x[0]+1/2, h0_ener(i)),
+
+ ax.annotate("", xy=(x[0]+1/2, h0_ener(i)-1/2),
+ xytext=(x[0]+1/2, h0_ener(i)),
arrowprops=dict(arrowstyle="<->"))
elif i==1:
- ax.text(x[0]+1/4, h0_ener(i-1)+1/3, r'$\hbar\omega$',
+ ax.text(x[0]+1/4, h0_ener(i-1)+1/3, r'$\hbar\omega$',
horizontalalignment='center', fontsize=14)
-
- ax.annotate("", xy=(x[0]+1/2, h0_ener(i)),
- xytext=(x[0]+1/2, h0_ener(i-1)),
+
+ ax.annotate("", xy=(x[0]+1/2, h0_ener(i)),
+ xytext=(x[0]+1/2, h0_ener(i-1)),
arrowprops=dict(arrowstyle="<->"))
-
+
ax.fill_between(x, h0_ener(i), ho_evec(x, i, no_states) + h0_ener(i), alpha=0.5)
-
+
ax.plot(x, V, 'k', linewidth=1) #plot harmonic potential
# Move left y-axis and bottim x-axis to centre, passing through (0,0)
@@ -194,8 +232,8 @@ ax.set_ylabel('$n$')
ax.set_yticks([1, 2])
ax.set_yticklabels(['$1$', '$2$'])
draw_classic_axes(ax, xlabeloffset=.2)
-T = np.linspace(0.01, 2)
-ax2.plot(T, 1/2 + 1/(np.exp(1/T)-1))
+temps = np.linspace(0.01, 2)
+ax2.plot(temps, 1/2 + 1/(np.exp(1/temps)-1))
ax2.set_ylim(bottom=0)
ax2.set_xlabel('$k_B T$')
ax2.set_xticks([0, 1])
@@ -224,15 +262,15 @@ def c_einstein(T, T_E=1):
x = T_E / T
return 3 * x**2 * np.exp(x) / (np.exp(x) - 1)**2
-T = np.linspace(0.01, 1.5, 500)
+temps = np.linspace(0.01, 1.5, 500)
fig, ax = pyplot.subplots()
-ax.plot(T, c_einstein(T)/3)
-ax.fill_between(T, c_einstein(T)/3, 1, alpha=0.5)
+ax.plot(temps, c_einstein(temps)/3)
+ax.fill_between(temps, c_einstein(temps)/3, 1, alpha=0.5)
ax.set_ylim(bottom=0, top=1.2)
ax.set_xlabel('$T$')
-ax.set_ylabel(r'$\omega$')
+ax.set_ylabel(r'$C$')
ax.set_xticks([1])
ax.set_xticklabels([r'$\hbar \omega/k_B$'])
ax.set_yticks([1])
@@ -241,28 +279,34 @@ pyplot.hlines([1], 0, 1.5, linestyles='dashed')
draw_classic_axes(ax)
```
-The dashed line signifies the classical value, $k_{\rm B}$. Shaded area $=\frac{1}{2}\hbar\omega$, the zero point energy that cannot be removed through cooling.
+The dashed line is the classical value, $k_{\rm B}$.
+Shaded area $=\frac{1}{2}\hbar\omega$, the zero point energy that cannot be removed through cooling.
-This is for just one atom. In order to obtain the heat capacity of a full material, we would have to multiply $C$ (or $\bar{\varepsilon}$) by $3N$, _i.e._ the number of harmonic oscillators according to Einstein model.[^1]
+This is for just one atom. In order to obtain the heat capacity of a full material, we would have to multiply $C$ (or $\bar{\varepsilon}$) by $3N$, _i.e._ the number of harmonic oscillators according to Einstein model.
```python
-# Data from Einstein's paper
-T = [222.4, 262.4, 283.7, 306.4, 331.3, 358.5, 413.0, 479.2, 520.0, 879.7, 1079.7, 1258.0]
-c = [0.384, 0.578, 0.683, 0.798, 0.928, 1.069, 1.343, 1.656, 1.833, 2.671, 2.720, 2.781]
-
fit = curve_fit(c_einstein, T, c, 1000)
T_E = fit[0][0]
delta_T_E = np.sqrt(fit[1][0, 0])
fig, ax = pyplot.subplots()
ax.scatter(T, c)
+
temps = np.linspace(10, T[-1], 100)
ax.plot(temps, c_einstein(temps, T_E));
+
ax.set_xlabel('$T[K]$')
ax.set_ylabel('$C/k_B$')
ax.set_ylim((0, 3));
```
+## Conclusions
+
+1. The law of Dulong–Petit is an observation that all materials have $C≈3k_B$ per atom.
+2. Oscillations of atoms are *quantum*, and they *freeze* at a low temperature, leaving only zero-point motion
+3. Using Bose–Einstein distribution we explain how $C$ drops with $T$.
+
+
## Exercises
### Exercise 1: Heat capacity of a classical oscillator.
@@ -280,7 +324,7 @@ $$
$$
Z = \int_{-\infty}^{\infty}dp \int_{-\infty}^{\infty} dx e^{-\beta H(p,x)}.
$$
-2. Using the solution of 1., compute the expectation value of the energy, and the expectation value of .
+2. Using the solution of 1., compute the expectation value of the energy.
3. Compute the heat capacity. Check that you get the law of Dulong-Petit but with a different prefactor.
4. Explain the difference in the prefactor by considering the number of degrees of freedom.
@@ -312,4 +356,6 @@ Naturally occurring lithium has [two stable isotopes](https://en.wikipedia.org/w
3. Write down the total energy of lithium at a temperature $T$ by modifying the Einstein model.
4. Compute the heat capacity of lithium as a function of $T$.
-[^1]: The data in this plot is the same as what Einstein used, but the curve in this plot is improved compared to what Einstein did, see [this blog post](https://quantumtinkerer.tudelft.nl/blog/footsteps-of-einstein/) for the backstory.
+
+[^1]: Data source: [Wikipedia](https://en.wikipedia.org/wiki/Heat_capacities_of_the_elements_(data_page)), mainly the CRC Handbook of Chemistry and Physics.
+[^2]: The data in this plot is the same as what Einstein used, but the curve in this plot is improved compared to what Einstein did, see [this blog post](https://quantumtinkerer.tudelft.nl/blog/footsteps-of-einstein/) for the backstory.
diff --git a/src/elements.json b/src/elements.json
new file mode 120000
index 0000000000000000000000000000000000000000..f712a76a363b566e81b275087371f8db415c3590
--- /dev/null
+++ b/src/elements.json
@@ -0,0 +1 @@
+../code/elements.json
\ No newline at end of file