14_doping_and_devices_solutions.md

from matplotlib import pyplot as plt 
import numpy as np
from math import pi

Solutions for lecture 14 exercises

Exercise 1: Crossover between extrinsic and intrinsic regimes

Subquestion 1

Law of mass action:

$$n_e n_h = \frac{1}{2} \left(\frac{k_BT}{\pi\hbar^2}\right)^3 (m_e^{\ast}m_h^{\ast})^{3/2}e^{-\beta E_{gap}}$$

Charge balance condition:

$$n_e - n_h + n_D - n_A = N_D - N_A$$

Subquestion 2

Since

$E_G \gg k_B T$

, we can only use the law of mass action. But the question offers us another piece of information - we are around

$|N_D-N_A| \approx n_i$

. That means that we are near the transition between extrinsic and intrinsic regimes. Because the dopants stop being ionized at very low temperatures (see next exercise), we can neglect

$n_D$

and

$n_A$

in this exercise, just like in the lecture. Writing

$n_e n_h = n_i^2$

and

$n_e - n_h = N_D - N_A$

and solving these together, we obtain

\begin{align} n_{e} = \frac{1}{2}(\sqrt{D^2+4n_i^2}+D),\ n_{h} = \frac{1}{2}(\sqrt{D^2+4n_i^2}-D) \end{align}

where

$D = N_D - N_A$

.

For

$n_i \gg |N_D - N_A|$

we recover the intrinsic regime, while the opposite limit gives the extrinsic expressions.

Subquestion 3

If

$D<<n_i$

, then the doping is not important and results of intrinsic are reproduced. Contrarily, if

$D>>n_i$

, it's mostly the doping that determines

$n_e$

and

$n_h$

. The thermal factor becomes unimportant. Check both cases with lecture notes approximated solutions by doing a Taylor expansion.

Exercise 2: Donor ionization

Subquestion 1

If all the dopants are ionized (

$n_D=0$

), the Fermi level gets shifted up towards the conduction band.

This result can be obtained when using results in Exercise 1 - Subquestion 2 and the following:

$$n_e - n_h = N_D - N_A$$

??? hint "To find

$E_F$

" Solve now for

$E_F$

using

$n_e$

and

$n_h$

expressions obtained in the previous lecture.

Subquestion 2

Now,

$$n_D = N_D\frac{1}{e^({E_D-E_F})/k_BT+1}$$

Subquestion 3

Because not all dopants are ionized, the charge conservation eq. becomes:

$$n_e - n_h + n_D = N_D - N_A$$

Doing the same as in subquestion 1, an expression for

$E_F$

can be found.

??? hint "Values" For Germanium at

$T=300K$

,

$n_i = 2.4 \times 10^{13} cm^{-3}$

This can be obtained when plugging

$m_e^{\ast}=0.55 m_e$

,

$m_h^{\ast}=0.37 m_e$

and

$T=300K$

in the results here.

Exercise 3: Performance of a diode

Subquestion 1

Intrinsic semiconductors have no impurities. Adding dopant atoms creates extra unbounded electrons/holes depending on the n/p dopant atom added. Impurity eigenstates appear and the

$E_F$

level shifts (up/down for added donors/acceptors).

To make a diode a p-n junction is needed (extrinsic semiconductors). Drawing a diagram is very helpful.

Subquestion 2

Under reverse bias only two processes carry out current: electrons that may be thermally excited into the conduction band (p-doped side) and holes that may be thermally excited into the valence band (n-doped side).

Subquestion 3

$$I_s(T) \propto e^{-E_{gap}/k_BT}$$

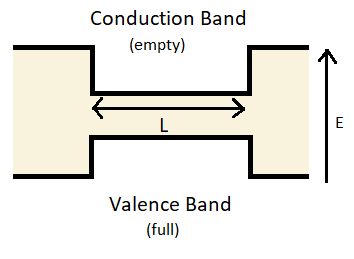
Exercise 4: Quantum well heterojunction in detail

Subquestion 1

• Include the energy bands here. You can find them at the book's section 18.2

Subquestion 2

This a "particle in a box" problem.

\begin{align} -\frac{\hbar^2}{2m_e^{\ast}} \nabla^2 \Psi_e &= (E_e-E_c)\Psi_e\ -\frac{\hbar^2}{2m_h^{\ast}} \nabla^2 \Psi_h &= (E_v-E_h)\Psi_h \end{align}

Subquestion 3

\begin{align} E_e = E_c + \frac{\hbar^2}{2m_e^{\ast}} ((\frac{\pi n}{L})^2+k_x^2+k_y^2) E_h = E_v - \frac{\hbar^2}{2m_h^{\ast}} ((\frac{\pi n}{L})^2+k_x^2+k_y^2)

Subquestion 4

This is a 2D electron/hole gas. Apply 2D density of states (constant).

\begin{align} g_e = \frac{4 \pi m_e^{\ast}}{\hbar^2},\ g_h = \frac{4 \pi m_h^{\ast}}{\hbar^2} \end{align}

Subquestion 5

L can be found here using previous subquestions. Setting

$$E_e - E_h - E_c + E_v = 1 eV = \frac{\hbar^2}{2}(\frac{\pi n}{L}^2+k_x^2+k_y^2) (\frac{1}{m_e^{\ast}}+\frac{1}{m_h^{\ast}})$$

By choosing the correct

$n$

,

$k_x$

and

$k_y$

, L can be found as

$6.85$

nm approx.

Subquestion 6

For a laser one wants to fix the emission wavelength to a certain value. With this setup the band gap is "easy" to design (set by L, which is fixed).

Subquestion 7

If donor impurities are put outside of the well (on both sides, for example) the donated electrons can reduce their energies by falling into the well, but the ionized dopants remain behind. This gives an advanttage because an extremely high mobility for electrons can be obtained within the quantum well (there are no ionized dopants in the well to scatter off of). This is called modulation doping.