expand the law of Dulong-Petit

mkdocs.yml

@@ -46,6 +46,7 @@ markdown_extensions:
   - admonition
   - pymdownx.details
   - abbr
+  - footnotes
 
 extra_javascript:
   - 'https://cdn.plot.ly/plotly-latest.min.js'

src/1_einstein_model.md

@@ -10,9 +10,7 @@ from common import draw_classic_axes, configure_plotting
 configure_plotting()
 ```
 
-# Lecture 1 – Phonons and specific Heat
-_(based on chapter 2 of the book)_  
-Exercises: 2.3, 2.4, 2.5, 2.6, 2.8
+_(based on chapter 2.1 of the book)_
 
 !!! summary "Learning goals"
 
@@ -22,11 +20,50 @@ Exercises: 2.3, 2.4, 2.5, 2.6, 2.8
     - Compute the expected particle number, energy, and heat capacity of a quantum harmonic oscillator (a single boson)
     - Write down the total thermal energy of a material
 
-### Einstein model
-Before solid state physics: heat capacity per atom $C=3k_{\rm B}$ (Dulong-Petit). Each atom is (classical) harmonic oscillator in three directions. Experiments showed that this law breaks down at low temperatures, where $C$ reduces to zero ($C\propto T^3$).
+## Einstein model
+
+### Classical limit
+
+An empirical observation:
+
+> The law of Dulong-Petit (1819): In most materials heat capacity per atom $C \approx 3k_B$
+
+![Heat capacity of chemical elements](https://upload.wikimedia.org/wikipedia/commons/6/6b/GraphHeatCapacityElements_SelectedRange.png)
+
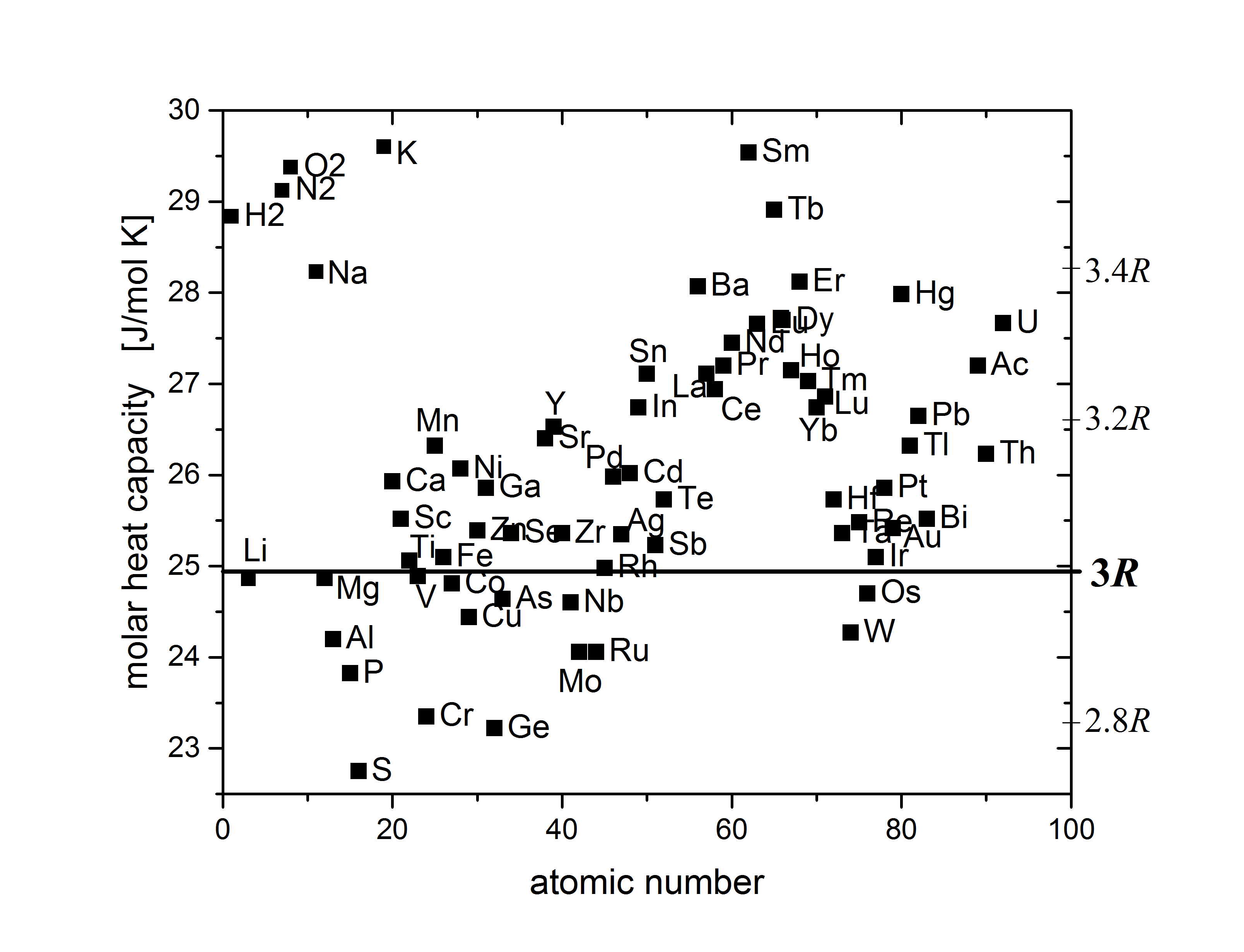
+??? info "source"
+
+    By Nick B. - Own work, [CC BY-SA 4.0](https://creativecommons.org/licenses/by-sa/4.0 "Creative Commons Attribution-Share Alike 4.0"), [Link](https://commons.wikimedia.org/w/index.php?curid=54031939)
+
+To explain assume that each atom is a classical harmonic oscillator in 3D.
+This gives 6 degrees of freedom, each contributing $k_B/2$ to the heat capacity.
+
+### Problem
+
+Experiments showed that this law breaks down at low temperatures, so Einstein was facing the mystery of this measurement:
+
+```python
+# Data from Einstein's paper
+T = [222.4, 262.4, 283.7, 306.4, 331.3, 358.5, 413.0, 479.2, 520.0, 879.7, 1079.7, 1258.0]
+c = [0.384, 0.578, 0.683, 0.798, 0.928, 1.069, 1.343, 1.656, 1.833, 2.671, 2.720, 2.781]
+
+fig, ax = pyplot.subplots()
+ax.scatter(T, c)
+ax.set_xlabel('$T[K]$')
+ax.set_ylabel('$C/k_B$')
+ax.set_ylim((0, 3));
+```
+
+So there is:
+
+* Strong temperature dependence of $C$
+* At high temperature the law of Dulong–Petit works
+* At low $T$, $C \rightarrow 0$
+
+### Quantum oscillator
 
 This can be explained by considering a _quantum_ harmonic oscillator:
-![](figures/harmonic.svg)
+
+![Wave functions and energies of a harmonic oscillator](figures/harmonic.svg)
 
 $$\varepsilon_n=\left(n+\frac{1}{2}\right)\hbar\omega$$
 
@@ -98,7 +135,7 @@ draw_classic_axes(ax)
 
 The dashed line signifies the classical value, $k_{\rm B}$. Shaded area $=\frac{1}{2}\hbar\omega$, the zero point energy that cannot be removed through cooling.
 
-This is for just one atom. In order to obtain the heat capacity of a full material, we would have to multiply $C$ (or $\bar{\varepsilon}$) by $3N$, _i.e._ the number of harmonic oscillators according to Einstein model.
+This is for just one atom. In order to obtain the heat capacity of a full material, we would have to multiply $C$ (or $\bar{\varepsilon}$) by $3N$, _i.e._ the number of harmonic oscillators according to Einstein model.[^1]
 
 ```python
 # Data from Einstein's paper
@@ -136,7 +173,7 @@ $$
 Z = \int_{-\infty}^{\infty}dp \int_{-\infty}^{\infty} dx e^{-\beta H(p,x)}.
 $$
 2. Using the solution of 1., compute the expectation value of the energy, and the expectation value of .
-3. Compute the heat capacity. Check that you get the law of Dulong-Petit but with a different prefactor. 
+3. Compute the heat capacity. Check that you get the law of Dulong-Petit but with a different prefactor.
 4. Explain the difference in the prefactor by considering the number of degrees of freedom.
 
 
@@ -165,4 +202,6 @@ Naturally occurring lithium has [two stable isotopes](https://en.wikipedia.org/w
 1. Assume that the strength of the returning force $k$ experienced by each atom is the same. What is the difference in the oscillation frequencies of different isotopes of lithium in the lithium crystal?
 2. Write down the total energy of lithium assuming that all $^6$Li atoms are in $n=2$ vibrational state, and all $^7$Li atoms are in $n=4$ vibrational state.
 3. Write down the total energy of lithium at a temperature $T$ by modifying the Einstein model.
-4. Compute the heat capacity of lithium as a function of $T$.
+4. Compute the heat capacity of lithium as a function of $T$.
\ No newline at end of file
+
+[^1]: The data in this plot is the same as what Einstein used, but the curve in this plot is improved compared to what Einstein did, see [this blog post](https://quantumtinkerer.tudelft.nl/blog/footsteps-of-einstein/) for the backstory.

src/2_debye_model.md

@@ -10,6 +10,8 @@ from common import draw_classic_axes, configure_plotting
 configure_plotting()
 ```
 
+_(based on chapter 2.2 of the book)_
+
 !!! summary "Learning goals"
 
     After this lecture you will be able to:
@@ -170,7 +172,7 @@ Explain your answer.
 4. At low $T$, show that $C_V=KT^{n}$. Find $n$. Express $K$ as a definite integral.
 
 ###  Exercise 3: Different phonon modes
-During the lecture we derived the low-temperature heat capacity assuming that all the phonons have the same sound velocity $v$. 
+During the lecture we derived the low-temperature heat capacity assuming that all the phonons have the same sound velocity $v$.
 In reality the longitudinal and transverse modes have different sound velocities (see [Wikipedia](https://en.wikipedia.org/wiki/Sound#Longitudinal_and_transverse_waves) for an illustration of different sound wave types).
 
 Assume that there are two types of excitations:
@@ -188,4 +190,4 @@ How does this change the Debye result for the heat capacity?
 
 ??? hint
 
-    Write down the total energy as an integral over $k$, then change the integration variables so that the spherical symmetry of the integrand is restored.
+    Write down the total energy as an integral over $k$, then change the integration variables so that the spherical symmetry of the integrand is restored.
\ No newline at end of file